Heap
우선순위 큐를 위하여 만들어진 자료구조로 완전 이진 트리의 일종이다. 데이터들중 최댓값 / 최솟값을 빠르게 찾아낼수 있다.
힙은 완전한 정렬이아닌 반정렬 상태로 유지되어진다 (상위레벨은 하위레벨보다 크거나 작다.)
종류
- 최대힙
부모노드의 키값 >= 자식노드의 키값
루트노드에 최대값이 들어간다. - 최소힙
부모노드의 키값 <= 자식노드의 키값
루트노드에 최소값이 들어간다.
Heap 의 형태
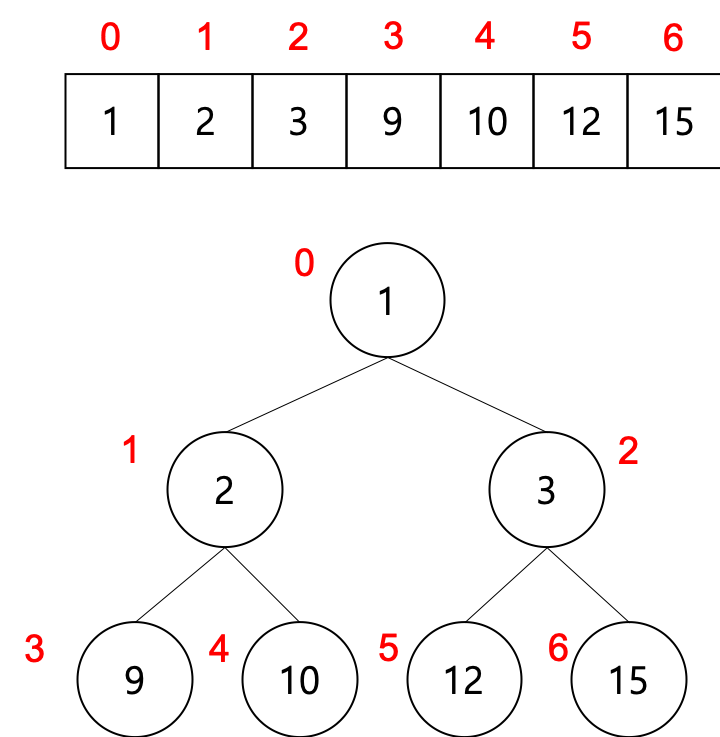
다음과 같은 형태를 띄며 (부모노드가 n) 라면, (자식노드는 2n+1) 이 된다.
Heap Insert
힙에 데이터를 삽입할때부터 정렬을 하면서 넣어줘야한다. 기본적으로 Insert시 마지막 Index에 Insert를 하게되며 단계적인 부모노드와의 비교를 통해 데이터 레벨을 올려서 정리한다.
Heap Delete
힙에 데이터삭제는 루트노드를 삭제함으로써 최대값 혹은 최소값을 추출해 낼수있다. 삭제할때도 마찬가지로 루트노트 삭제후 단계적인 자식노드들간 비교를 통해 데이터 레벨을 올려서 정리한다. 여기서 주의할점은 마지막으로 변경된 자식노드의 자리에는 마지막 노드의 값이 들어가 힙을 유지시킨다.
Java 최소 Heap 구현
Class Heap{
int[] heapArr;
int heapsize=0;
public void insertHeap(int n){
int child = heapsize++;
int parent = (child-1)/2;
while(child!=0){
if(heapArr[child]<heapArr[parent]){ //부모노드와의 비교
heapArr[child] = heapArr[parent];
child = parent;
parent = (child-1)/2;
}else{
break;
}
}
hearArr[child]=n;
}
public int deleteHeap(){
int result = heapArr[0];
int child = 1;
int parent = 0;
while(child<heapsize){
if(child<(heapsize-1)&&heapArr[child]>heapArr[child+1]){ //자식노드간 비교
child += 1;
}
heapArr[parent] = heapArr[child];
parent = child;
child = child*2+1;
}
heapArr[parent] = heapArr[--heapsize]; //마지막노드 이동
return result;
}
}