Hash Function
해쉬함수는 임의이 길이의 데이터를 고정된 길이의 데이터로 매핑시키는 함수이다. 해시를 이용해 데이터를 정리하면 정렬을 하지 않고도 빠른검색 및 삽입이 충분히 가능해진다.
예를들자면 [1,4,7,13,16]의 데이터 가 있는상황에서 크기가 7인 배열에 정리하고자 한다면 해쉬함수를 %7으로 설정해두면
1%7 = 1
4%7 = 4
7%7 = 0
13%7 = 6
16%7 = 2
다음과같은 결과값으로 나타내질수 있고, 위의 나머지 결과값을 index라고 생각해보면 데이터는 다음과 같이 정리될수 있다.
[0] : 7
[1] : 1
[2] : 16
[3]
[4] : 4
[5]
[6] : 13
다음과 같이 정리된 테이블을 해시테이블이라 하며, 값을통해 index값을 바로 찾아낼수 있어 데이터 검색에 O(1)의 시간복잡도를 가진다.
Hash Coluusion
위의 데이터같은 상황에서 14값을 추가로 저장한다고 생각해보자. 14%7 = 0으로, 현재 [0] : 7 해시테이블에 데이터가 겹쳐지게 된다. 임의의 데이터를 한정된 길이의 데이터로 매핑시키다보니 데이터의 주소가 겹쳐지는 일은 필연적으로 발생한다. 이러한 현상을 해시 충돌이라 한다. 따라서 데이터의 값을 완전히 보장하기 위해 해시함수는 최대한 충돌을 피할 수 있는 함수가 되어야하나 그것도 완전히 방지하기는 어려우므로, 그를 보완하기 위한 다양한 방법들이있다.
- Chaining
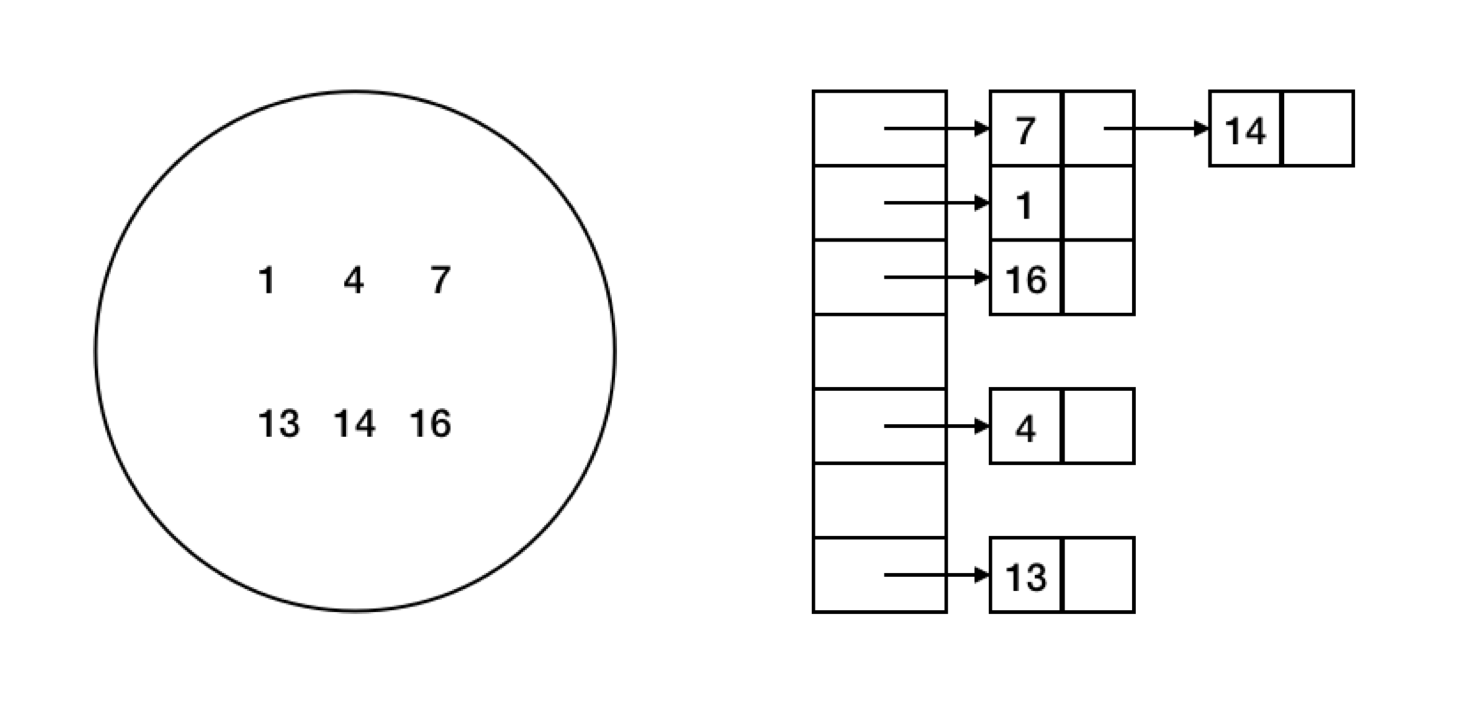
다음과 같이 해시테이블 + 연결리스트 방식으로 정리하는 방법이다. 이 방법의경우 충돌을 허용하면서 정리하는 방식이라고 할 수 있다. 다만 이경우 적재율이 높아질수록 연결 리스트가 길어져 탐색에 최대 O(n)의 시간복잡도를 가질수 있다.
- 좋은 해시함수 만들기 충돌을 피하기위한 가장 근본적인 방법으로, 충돌이 일어나지않는 ‘좋은’함수를 만들어 내는것이다. 이를 위해 좋은해시함수를 만들기위한 몇가지 룰이있는데 이것을 Simple uniform hash라 하며 룰은 다음과 같다.
1. 계산된 해쉬값들은 해시테이블에 동일한 확률로 발생한다.
2. 해쉬값들은 서로 연관성을 갖지 않는다.
이를 적용하는 대표적인 함수로 위에서 이용한 나머지연산을 이용한 division method 가 있다. 보통 최적의 테이블 크기 설정은 키의 갯수의 3배로써 2의 지수승에 근접한 소수로 잡는것을 최고의 효율을 보장한다고 한다.
- Open addressing
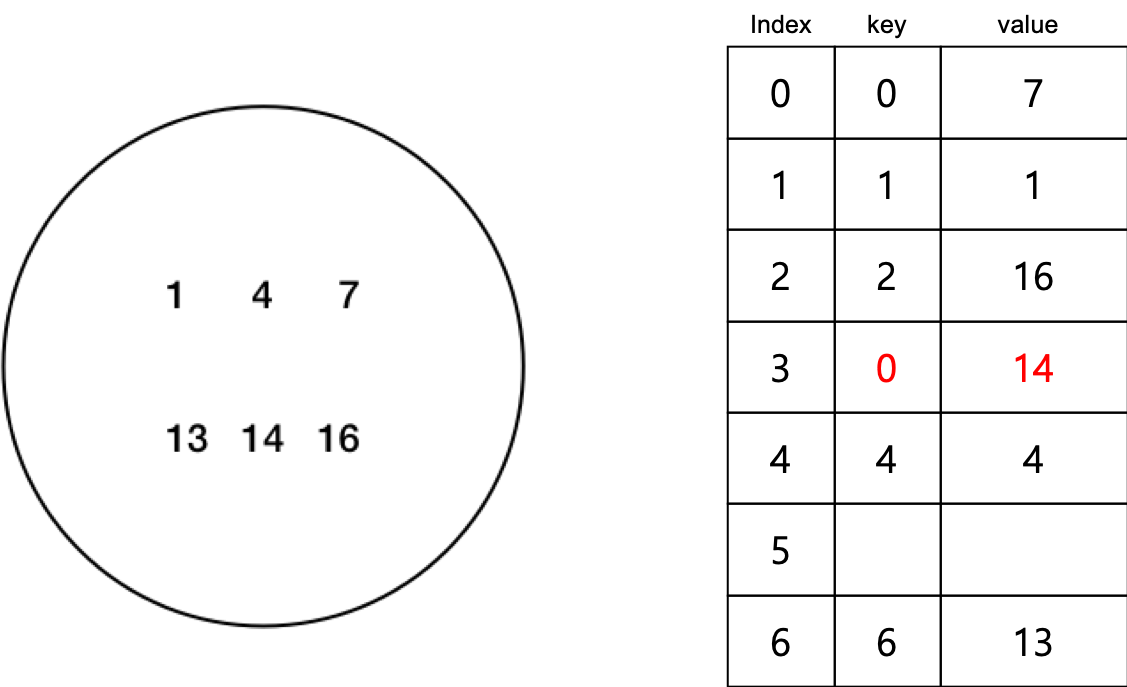
위는 Open addressing중 Linear probing 방식으로 위 그림과 같이 정해진 주소에 정해진 값이 들어가지 않을 수 있는 말그대로 열린 주소값 방식이다.
해시테이블내에서 해시키값이 Index값으로 보장되지 않으므로 데이터 값과 해시 키값을 함께 저장해주는데, 데이터 삽입시 key 값이 중복될 경우 다음 Index로 넘어가 저장시키는 방식이다.
따라서 검색을 해서 원하는 데이터가 나오지 않는경우 뒤의 index를 검색해서 같은 키가 나오거나 key가 없을때 까지 검색을 진행 하게되어 최대 O(n)의 시간복잡도를 가질수 있다.
이외에도 상황에 맞는 다양한 해시테이블이 있다.